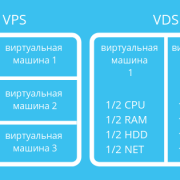
Mcmc-сэмплинг для тех, кто учился, но ничего не понял
Содержание:
Oversampling
И децимацию и интерполяцию уже упомянули. Вроде бы и всё. Но в плагинах часто можно увидеть термин oversampling, да ещё и с каким-то настройками. Давайте разбираться.
Есть такое определение как «Дискретизация сигналов с запасом по частоте дискретизации». То есть применяется дискретизация сигнала на частоте, в несколько раз превышающей частоту Котельникова (предел Найквиста) с последующей децимацией. Вот она и называется в англоязычной литературе термином oversampling.
Например, возьмём сигнал с шириной полосы или самой высокой частотой B = 100 Гц. Зная, что есть предел Найквиста берётся частота дискретизации в 2 раза больше — 200 Гц (100 × 2). При oversampling 4x частота дискретизации в четыре раза превышает частоту дискретизации 800 Гц (200 × 4). В итоге фильтр anti — aliasing работает в переходной полосе 300 Гц. То есть получается следующая формула (( f s / 2) — B = (800 Гц / 2) — 100 Гц = 300 Гц.
Что даёт такой тип дискретизации сигнала?
- Возможность использовать АЦП (аналого-цифровой преобразователь) с меньшей разрядностью.
- Возможность использовать более простой и дешёвый аналоговый фильтр для защиты от наложения спектров.
- Подобная передискретизация способна улучшить разрешение и отношение сигнал / шум, а также может помочь избежать наложения спектров и фазовых искажений путем ослабления требований к характеристикам фильтра сглаживания.
Аналогичный подход применяется и при восстановлении сигнала по его отсчётам.
Calculating Average Power¶
For a discrete complex signal, i.e., one we have sampled, we can find the average power by taking the magnitude of each sample, squaring it, and then finding the mean:
Remember that the absolute value of a complex number is just the magnitude, i.e.,
In Python, calculating the average power will look like:
avg_pwr = np.mean(np.abs(x)**2)
Here is a very useful trick for calculating the average power of a sampled signal.
If your signal has roughly zero mean–which is usually the case in SDR (we will see why later)–then the signal power can be found by taking the variance of the samples. In these circumstances, you can calculate the power this way in Python:
avg_pwr = np.var(x) # (signal should have roughly zero mean)
Introduction
Here’s a scenario I’m sure you are familiar with. You download a relatively big dataset and are excited to get started with analyzing it and building your machine learning model. And snap – your machine gives an “out of memory” error while trying to load the dataset.
It’s happened to the best of us. It’s one of the biggest hurdles we face in data science – dealing with massive amounts of data on computationally limited machines (not all of us have Google’s resource power!).
So how can we overcome this perennial problem? Is there a way to pick a subset of the data and analyze that – and that can be a good representation of the entire dataset?

Yes! And that method is called sampling. I’m sure you’ve come across this term a lot during your school/university days, and perhaps even in your professional career. Sampling is a great way to pick up a subset of the data and analyze that. But then – should we just pick up any subset randomly?
Well, we’ll discuss that in this article. We will talk about eight different types of sampling techniques and where you can use each one. This is a beginner-friendly article but some knowledge about descriptive statistics will serve you well.
If you’re new to statistics and data science, I encourage you to check out our two popular courses:
- Introduction to Data Science
- Applied Machine Learning: Beginner to Professional
Моделирование
Мы можем полностью отойти от теоретического решения и решить задачу «в лоб». Благодаря языку R теперь это сделать очень просто. Чтобы ответить на вопрос, в какую мы ошибку получим при сэмплировании, можно просто сделать тысячу сэмплирований и посмотреть, какую ошибку мы получаем.
Подход такой:
- Берем разные коэффициенты конверсии (от 0.01% до 50%).
- Берем 1000 сэмплов по 10, 100, 1000, 10000, 50000, 100000, 250000, 500000 элементов в выборке
- Считаем коэффициент конверсии по каждой группе сэмплов (1000 коэффициентов)
- Строим гистограмму по каждой группе сэмплов и определяем, в каких пределах лежат 60%, 80% и 90% наблюдаемых коэффициентов конверсии.
Код на R генерирующий данные:
В результате мы получаем следующую таблицу (дальше будут графики, но детали лучше видны в таблице).
| Коэффициент конверсии | Размер сэмпла | 5% | 10% | 20% | 80% | 90% | 95% |
|---|---|---|---|---|---|---|---|
| 0.0001 | 10 | ||||||
| 0.0001 | 100 | ||||||
| 0.0001 | 1000 | 0.001 | |||||
| 0.0001 | 10000 | 0.0002 | 0.0002 | 0.0003 | |||
| 0.0001 | 50000 | 0.00004 | 0.00004 | 0.00006 | 0.00014 | 0.00016 | 0.00018 |
| 0.0001 | 100000 | 0.00005 | 0.00006 | 0.00007 | 0.00013 | 0.00014 | 0.00016 |
| 0.0001 | 250000 | 0.000072 | 0.0000796 | 0.000088 | 0.00012 | 0.000128 | 0.000136 |
| 0.0001 | 500000 | 0.00008 | 0.000084 | 0.000092 | 0.000114 | 0.000122 | 0.000128 |
| 0.001 | 10 | ||||||
| 0.001 | 100 | 0.01 | |||||
| 0.001 | 1000 | 0.002 | 0.002 | 0.003 | |||
| 0.001 | 10000 | 0.0005 | 0.0006 | 0.0007 | 0.0013 | 0.0014 | 0.0016 |
| 0.001 | 50000 | 0.0008 | 0.000858 | 0.00092 | 0.00116 | 0.00122 | 0.00126 |
| 0.001 | 100000 | 0.00087 | 0.00091 | 0.00095 | 0.00112 | 0.00116 | 0.0012105 |
| 0.001 | 250000 | 0.00092 | 0.000948 | 0.000972 | 0.001084 | 0.001116 | 0.0011362 |
| 0.001 | 500000 | 0.000952 | 0.0009698 | 0.000988 | 0.001066 | 0.001086 | 0.0011041 |
| 0.01 | 10 | 0.1 | |||||
| 0.01 | 100 | 0.02 | 0.02 | 0.03 | |||
| 0.01 | 1000 | 0.006 | 0.006 | 0.008 | 0.013 | 0.014 | 0.015 |
| 0.01 | 10000 | 0.0086 | 0.0089 | 0.0092 | 0.0109 | 0.0114 | 0.0118 |
| 0.01 | 50000 | 0.0093 | 0.0095 | 0.0097 | 0.0104 | 0.0106 | 0.0108 |
| 0.01 | 100000 | 0.0095 | 0.0096 | 0.0098 | 0.0103 | 0.0104 | 0.0106 |
| 0.01 | 250000 | 0.0097 | 0.0098 | 0.0099 | 0.0102 | 0.0103 | 0.0104 |
| 0.01 | 500000 | 0.0098 | 0.0099 | 0.0099 | 0.0102 | 0.0102 | 0.0103 |
| 0.1 | 10 | 0.2 | 0.2 | 0.3 | |||
| 0.1 | 100 | 0.05 | 0.06 | 0.07 | 0.13 | 0.14 | 0.15 |
| 0.1 | 1000 | 0.086 | 0.0889 | 0.093 | 0.108 | 0.1121 | 0.117 |
| 0.1 | 10000 | 0.0954 | 0.0963 | 0.0979 | 0.1028 | 0.1041 | 0.1055 |
| 0.1 | 50000 | 0.098 | 0.0986 | 0.0992 | 0.1014 | 0.1019 | 0.1024 |
| 0.1 | 100000 | 0.0987 | 0.099 | 0.0994 | 0.1011 | 0.1014 | 0.1018 |
| 0.1 | 250000 | 0.0993 | 0.0995 | 0.0998 | 0.1008 | 0.1011 | 0.1013 |
| 0.1 | 500000 | 0.0996 | 0.0998 | 0.1 | 0.1007 | 0.1009 | 0.101 |
| 0.5 | 10 | 0.2 | 0.3 | 0.4 | 0.6 | 0.7 | 0.8 |
| 0.5 | 100 | 0.42 | 0.44 | 0.46 | 0.54 | 0.56 | 0.58 |
| 0.5 | 1000 | 0.473 | 0.478 | 0.486 | 0.513 | 0.52 | 0.525 |
| 0.5 | 10000 | 0.4922 | 0.4939 | 0.4959 | 0.5044 | 0.5061 | 0.5078 |
| 0.5 | 50000 | 0.4962 | 0.4968 | 0.4978 | 0.5018 | 0.5028 | 0.5036 |
| 0.5 | 100000 | 0.4974 | 0.4979 | 0.4986 | 0.5014 | 0.5021 | 0.5027 |
| 0.5 | 250000 | 0.4984 | 0.4987 | 0.4992 | 0.5008 | 0.5013 | 0.5017 |
| 0.5 | 500000 | 0.4988 | 0.4991 | 0.4994 | 0.5006 | 0.5009 | 0.5011 |
Посмотрим случаи с 10% конверсией и с низкой 0.01% конверсией, т.к. на них хорошо видны все особенности работы с сэмплированием.
При 10% конверсии картина выглядит довольно простой:

Точки — это края 5-95% доверительного интервала, т.е. делая сэмпл мы будем в 90% случаев получать CR на выборке внутри этого интервала. Вертикальная шкала — размер сэмпла (шкала логарифмическая), горизонтальная — значение коэффициента конверсии. Вертикальная черта — «истинный» CR.
Мы тут видим то же, что мы видели из теоретической модели: точность растет по мере роста размера сэмпла, при этом одна довольно быстро «сходится» и сэмпл получает результат близкий к «истинному». Всего на 1000 сэмпле мы имеем 8.6% — 11.7%, что для ряда задач будет достаточно. А на 10 тысячах уже 9.5% — 10.55%.
Куда хуже дела обстоят с редкими событиями и это согласуется с теорией:

У низкого коэффициента конверсии в 0.01% принципе проблемы на статистике в 1 млн наблюдений, а с сэмплами ситуация оказывается еще хуже. Ошибка становится просто гигантской. На сэмплах до 10 000 метрика в принципе не валидна. Например, на сэмпле в 10 наблюдений мой генератор просто 1000 раз получил 0 конверсию, поэтому там только 1 точка. На 100 тысячах мы имеем разброс от 0.005% до 0.0016%, т.е мы можем ошибаться почти в половину коэффициента при таком сэмплировании.
Также стоит отметить, что когда вы наблюдаете конверсию такого маленького масштаба на 1 млн испытаний, то у вас просто большая натуральная ошибка. Из этого следует, что выводы по динамике таких редких событий надо делать на действительно больших выборках иначе вы просто гоняетесь за призраками, за случайными флуктуациями в данных.
Выводы:
Сэмплирование рабочий метод для получения оценок
Точность сэмплов растет при росте размера сэмпла и падает при снижении коэффициента конверсии.
Точность оценок можно смоделировать для вашей задачи и таким образом подобрать оптимальное сэмплирование для себя
Важно помнить, что редкие события плохо сэмплируют
В целом редкие события трудно анализировать, они без сэмплов требуют больших выборок данных.
Литература
- Tomas Mikolov, Kai Chen, Greg Corrado, and Jeffrey Dean. Efficient estimation
of word representations in vector space. CoRR, abs/1301.3781, - Tomas Mikolov, Ilya Sutskever, Kai Chen, Gregory S. Corrado, and Jeffrey Dean. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013. Proceedings of a meeting held December 5-8, 2013, Lake Tahoe, Nevada, United States, pages 3111–3119, 2013.
- Morin, F., & Bengio, Y. Hierarchical Probabilistic Neural Network Language Model. Aistats, 5, 2005.
- Jeffrey Pennington, Richard Socher, and Christopher D. Manning. GloVe: Global Vectors for Word Representation. 2014.
- Piotr Bojanowski, Edouard Grave, Armand Joulin, and Tomas Mikolov. Enriching word vectors
with subword information. arXiv preprint arXiv:1607.04606, 2016.
* Да, это специальная пасхалка для любителей творчества Энтони Бёрджеса.
Sampling thresholds
Default reports are not subject to sampling.
Ad-hoc queries of your data are subject to the following general thresholds for sampling:
- Analytics Standard: 500k sessions at the property level for the date range you are using
- Analytics 360: 100M sessions at the view level for the date range you are using
-
Queries may include events, custom variables, and custom dimensions and metrics. All other queries have a threshold of 1M
-
Historical data is limited to up to 14 months (on a rolling basis)
-
In some circumstances, you may see fewer sessions sampled. This can result from the complexity of your Analytics implementation, the use of view filters, query complexity for segmentation, or some combination of those factors. Although we make a best effort to sample up to the thresholds described above, it’s normal to sometimes see slightly fewer sessions returned for an ad-hoc query.
Population Distribution Marriages
Many inhabitants never married (yet), in which case marriages is zero. Other inhabitants married, divorced and remarried, sometimes multiple times. The histogram below shows the distribution of marriages over our 976 inhabitants.
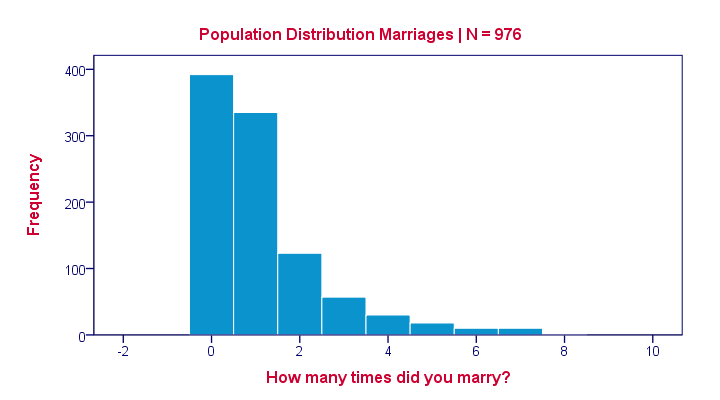
Note that the population distribution is strongly skewed (asymmetrical) which makes sense for these data. On average, people married some 1.1 times as shown by some descriptive statistics below.

These descriptives reemphasize the high skewness of the population distribution; the skewness is around 1.8 whereas a symmetrical distribution has zero skewness.
Методика
Вычислительная стоимость и адаптивная суперсэмплинг
Суперсэмплинг требует больших вычислительных ресурсов, поскольку требует гораздо большей памяти видеокарты и пропускной способности памяти , поскольку объем используемого буфера в несколько раз больше. Обойти эту проблему можно с помощью метода, известного как адаптивная суперсэмплинг , при котором суперсэмплинг подвергаются только пиксели на краях объектов.
Первоначально в каждом пикселе берутся только несколько образцов. Если эти значения очень похожи, только эти образцы используются для определения цвета. В противном случае используются другие. Результатом этого метода является то, что большее количество выборок рассчитывается только там, где это необходимо, что улучшает производительность.
Шаблоны суперсэмплинга
При отборе образцов в пределах пикселя положение образцов должно быть определено каким-то образом. Хотя количество способов, которыми это можно сделать, бесконечно, есть несколько обычно используемых способов.
Сетка
Самый простой алгоритм . Пиксель разбивается на несколько подпикселей, и образец берется из центра каждого. Это быстро и легко реализовать. Хотя, из-за регулярного характера выборки, наложение спектров все еще может происходить, если используется небольшое количество подпикселей.
Случайный
Также известный как стохастическая выборка, он позволяет избежать регулярной суперсэмплинга сетки. Однако из-за неравномерности рисунка в некоторых областях пикселя сэмплы оказываются ненужными, а в других — отсутствуют.
Диск Пуассона
Точечные выборки, созданные с использованием выборки диска Пуассона, и графическое представление минимального межточечного расстояния
Алгоритм выборки диска Пуассона размещает выборки случайным образом, но затем проверяет, что любые две не слишком близки. Конечным результатом является равномерное, но случайное распределение выборок. Однако вычислительное время, необходимое для этого алгоритма, слишком велико, чтобы оправдать его использование при рендеринге в реальном времени , если только сама выборка не требует больших вычислительных затрат по сравнению с позиционированием точек выборки или точки выборки не перемещаются для каждого отдельного пикселя.
Взволнованный
Модификация сеточного алгоритма для аппроксимации диска Пуассона. Пиксель разбивается на несколько подпикселей, но выборка берется не из центра каждого, а из случайной точки внутри подпикселя. Конгрегация все еще может происходить, но в меньшей степени.
Повернутая сетка
Используется сетка 2 × 2, но образец образца поворачивается, чтобы избежать выравнивания образцов по горизонтальной или вертикальной оси, что значительно улучшает качество сглаживания для наиболее часто встречающихся случаев. Для оптимального шаблона угол поворота арктангенциальный ( 1 2 ) (около 26,6 °), а квадрат растягивается в раз √ 5 2 .
Как организовать сэмплинг проект?
При организации btl проекта важно учесть несколько на первый взгляд простых, но в тоже время важных принципов подготовки мероприятия, от которых на прямую может зависеть их успех
Персонал
Поиск, обучение, контроль за промоутерами или консультантами, то есть основным персоналом на промо-акции является первостепенной задачей организаторов сэмплинг-проекта или мероприятия с любой другой механикой. Почему? Дело в том, что в рамках рекламной кампании на основе btl именно промоутер (консультант) является лицом бренда или продукта и от того, как выглядит персонал, насколько высоки его коммуникативные навыки и знания о самом продукте зависит успех конкретного промо проекта. К примеру, если при общении с потребителем персонал не сможет рассказать о преимуществах продукта в сравнении с конкурентами, будет выглядеть не опрятно или нецензурно выражаться, хамить посетителям торговой точки, то соответствующее мнение сложится не о конкретном человеке (промоутере), а о представляемом бренде в целом. Кроме того, от активности промо команды и от уровня профессионализма каждого ее члена зависит в целом успех мероприятия.
Место и время
Выбор места и времени проведения активности играет немаловажную роль
Причем важно непросто выбрать наиболее проходимую площадку, но и сделать акцент на целевую аудиторию. К примеру, если основным потребителем продукта являются люди пенсионного возраста, то нет смысла в реализации акции в вечернее время в торгово-развлекательных центрах, ведь в большинстве своем данная категория граждан в указанный временной период не посещает такие места, а вот люди молодого возраста наоборот наиболее активны в это время и им выбор места подходит
Контроль за проведением
Однако уделять внимание стоит не только планированию мероприятия, но и не забывать о контроле реализации. Пускать все на самотек не стоит
Конечно, доверять проверенному персоналу можно, но, тем не менее, следить за процессом, корректировать работу промоутеров в ходе акции, устраивать «планерки» в начале и «разбор полетов» в конце каждого акционного дня или периода – необходимо. Для чего? Чтобы подстраховаться, предотвратить возможные ошибки и казусные ситуации, которые могут повлиять не конечный результат проекта.
Потребитель
Думать об успехе проекта, но исключить из внимания потребности аудитории – непростительная ошибка. Суть любого промо проекта сводится к тому, чтобы прилечь и заинтересовать потребителя, а значит необходимо сделать все и даже больше, чтобы покупатель остался доволен. Как? Придумать интересный сценарий, креативные костюмы, сделать правильный выбор сэмплов.
К примеру, для продвижения крема для обуви можно просто раздавать бесплатные образцы в торговой точке, а можно устроить настоящий пункт очистки обуви, где каждый желающий самостоятельно или с помощью консультантов смог бы проверить новый продукт в действии и в тоже время получить пробник товара. Боитесь включать фантазию, так как это может отпугнуть покупателей? Подумайте о том, что отсутствие индивидуальности может привести к победе конкурентов, которые в свою очередь не побоялись и перешли от рассуждений к действиям!
Товар
Продвигаемый продукт должен быть доступен для целевой аудитории. Речь идет как о ценовой характеристике продукта, так и о его наличии в торговой точке, в которой происходит промо активность. В противном случае сэмплинг состоится, но не принесет желаемого эффекта.
Особенности применения сэмплинга
Кроме выбора собственно метода сэмплинга, который наилучшим образом подходит к решаемой задаче и используемым данным, аналитику требуется принять решение о некоторых особенностях его применения. Обычно это связано с выбором, будет ли реализован сэмплинг с возвратом или без, а также определить размер полученной выборки.
Сэмплинг с возвратом (заменой) — это методика построения выборок, при которой каждый объект исходной совокупности может быть выбран более, чем один раз. Т.е. предполагается что отбираемый объект не перемещается, а копируется в выборку, оставаясь в исходной совокупности.
Сэмплинг без возврата (замены) предполагает, что каждый объект совокупности может быть выбран только один раз. Т.е. объект перемещается из исходной совокупности в выборку.
Сэмплинг с возвратом используется в том случае, если количество уникальных объектов совокупности недостаточно для формирования выборки требуемого объема, что компенсируется возможностью многократного выбора объектов. Недостатком подхода является появление в выборке дубликатов. Таким образом, сэмплинг с заменой позволяет увеличить объем выборки, но не её репрезентативность.
Определение объёма выборки. Определение числа объектов, из которого будет состоять выборка, является важным элементом любого эмпирического исследования в статистике или анализе данных, по результатам которого должны быть сделаны вывод о свойствах совокупности на основе свойств выборки.
На практике объём выборки обычно определяется на основе затрат, времени или удобства сбора данных, а также необходимости достижения необходимой репрезентативности и полноты.
В заключении следует отметить, что несмотря на общепринятую схему классификации, которая наиболее часто приводится в литературе, методология сэмплинга не имеет чётких границ. Вообще говоря, к сэмплингу можно отнести любой метод отбора данных, который формирует выборки, с помощью которых пользователь может решать свои задачи. Например, в сэмплинге могут использоваться алгоритмы фильтрации строк.
При этом достижение репрезентативности, полноты и точности выборки не является приоритетным. Главное, чтобы она была полезной для решения практической задачи. Вопрос только в корректности построенных с её помощью моделей, сделанных выводах и обобщениях.
Другие материалы по теме:
Quadrature Sampling¶
The term “quadrature” has many meanings, but in the context of DSP and SDR it refers to two waves that are 90 degrees out of phase. Why 90 degrees out of phase? Consider how two waves that are 180 degrees out of phase are essentially the same wave with one multiplied by -1. By being 90 degrees out of phase they become orthogonal, and there’s a lot of cool stuff you can do with orthogonal functions. For the sake of simplicity, we use sine and cosine as our two sine waves that are 90 degrees out of phase.
Next let’s assign variables to represent the amplitude of the sine and cosine. We will use for the cos() and for the sin():
We can see this visually by plotting I and Q equal to 1:
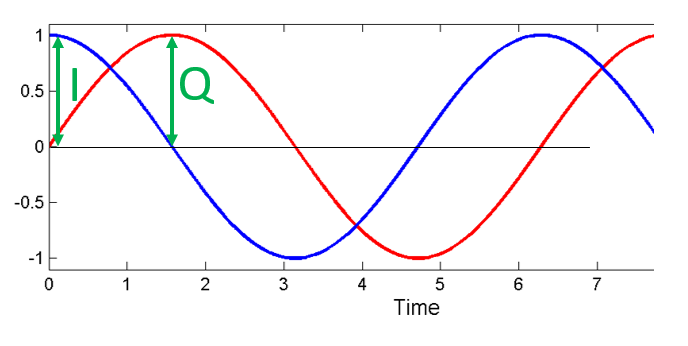
We call the cos() the “in phase” component, hence the name I, and the sin() is the 90 degrees out of phase or “quadrature” component, hence Q. Although if you accidentally mix it up and assign Q to the cos() and I to the sin(), it won’t make a difference for most situations.
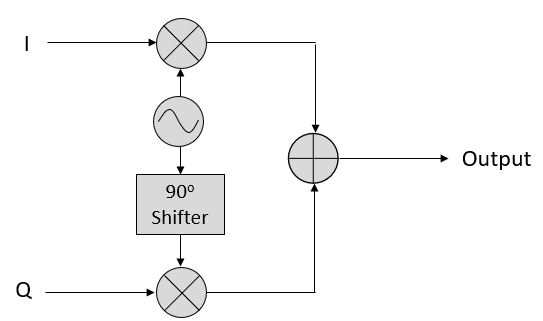
IQ sampling is more easily understood by using the transmitter’s point of view, i.e., considering the task of transmitting a RF signal through the air. What we do as the transmitter is add the sin() and cos(). Let’s say x(t) is our signal to transmit:
What happens when we add a sine and cosine? Or rather, what happens when we add two sinusoids that are 90 degrees out of phase? In the video below, there is a slider for adjusting I and another for adjusting Q. What is plotted are the cosine, sine, and then the sum of the two.

(The code used for this pyqtgraph-based Python app can be found here)
The important take-aways are that when we add the cos() and sin(), we get another pure sine wave with a different phase and amplitude. Also, the phase shifts as we slowly remove or add one of the two parts. The amplitude also changes. This is all a result of the trig identity: , which we will come back to in a bit. The “utility” of this behavior is that we can control the phase and amplitude of a resulting sine wave by adjusting the amplitudes I and Q (we don’t have to adjust the phase of the cosine or sine). For example, we could adjust I and Q in a way that keeps the amplitude constant and makes the phase whatever we want. As a transmitter this ability is extremely useful because we know that we need to transmit a sinusoidal signal in order for it to fly through the air as an electromagnetic wave. And it’s much easier to adjust two amplitudes and perform an addition operation compared to adjusting an amplitude and a phase. The result is that our transmitter will look something like this:
Виды сэмплинга
Сэмплинг — отличный способ стимулирования продаж в ритейле. Его организация в точках продаж позволяет подключать эмоции потенциальных покупателей и мотивирует их делать спонтанные покупки. Однако, сэмплинг не обязательно проводят на территории магазина или торгового центра. Некоторые компании предлагают образцы своей продукции прямо на улице. Ознакомьтесь подробнее с видами сэмплинга.
- Обмен (Switch-sampling). Подразумевает обмен наполовину пустой упаковки используемого товара на новый. Такой подход помогает клиенту сравнить качество аналогичных товаров.
- Сухой сэмплинг (dry sampling). Предполагает рекламу продукта в точке продажи. Потенциальным покупателям предлагают взять с собой пробник бальзама для волос, крема, зубной пасты или другого товара.
- Влажный сэмплинг (wet sampling). Предоставляет целевой аудитории возможность продегустировать товар на месте. Например, колбасные изделия, сыр, масло, йогурт и так далее.
- HoReCa сэмплинг (Hotel-Restaurant-Cafe sampling). Это дегустация алкогольных и безалкогольных напитков, а также сигарет. Такой сэмплинг чаще всего организовывают в ресторанах, кафе, гостиницах и преподносят как комплимент от заведения или подарок при заказе на определенную сумму.
- Домашний сэмплинг (house-to-house sampling). Предполагает рассылку примеров товара почтой. Это может быть мини-версия продукта или печатная реклама с образцами и многое другое.
Теперь, когда вы знаете виды сэмплинга, самое время узнать, как правильно его организовать.
Как организовать сэмплинг
- Установите цели и задачи сэмплинга
- Подберите продукт и установите объем сэмпла
- Выберите время проведения сэмплинга
- Выберите место проведения сэмплинга
- Соберите команду промоутеров
Чтобы организовать эффективный сэмплинг, воспользуйтесь следующими полезными рекомендациями.
Установите цели и задачи сэмплинга. Прежде чем приступать к организационным вопросам, подумайте, зачем вам нужна эта акция, чего вы хотите достичь с ее помощью. Подготовьте маркетинговый план и по пунктам пропишите пути достижения каждой задачи.
Подберите продукт и установите объем сэмпла
В этом вопросе важно полагаться на интересы и предпочтения целевой аудитории. Тщательно продумайте, что вы будете предлагать, как и в каком количестве
Пропишите расходы, необходимые для организации сэмплинга.
Выберите время проведения сэмплинга. Установите, когда лучше всего взаимодействовать с целевой аудиторией. Сэмплинг может проводится на протяжении всего дня или в какие-то определенные часы. Такой подход позволит сконцентрировать усилия на потенциальных покупателях и не распылять свои ресурсы.
Выберите место проведения сэмплинга. На основании данных о своей целевой аудитории выявите наиболее релевантные точки проведения акции. Подумайте, где больше всего ваших потенциальных покупателей. При этом помните, что клиент должен иметь возможность купить товар, иначе он может передумать и все усилия будут сведены к минимуму.
Соберите команду промоутеров. В этом вопросе важно учесть пол, возраст и другие характеристики, которые могут влиять на уровень доверия вашей целевой аудитории.
При правильном подходе сэмплинг способен увеличить объем продаж на 200-300%. Однако, эффективность не всегда можно измерить в денежном эквиваленте, ведь ознакомление целевой аудитории с продукцией это еще и работа на перспективу. Используйте инструменты ATL и BTL-рекламы, задействуйте мессенджеры и социальные сети, чтобы увеличить количество точек контакта с клиентом.